純水流量計傳感器檢測原理及權(quán)函數(shù)仿真與分析
點擊次數(shù):1985 發(fā)布時間:2021-01-16 12:43:56
摘要:在非理想流場條件下,異徑純水流量計傳感器將產(chǎn)生較大的測量誤差。提高傳感器權(quán)函數(shù)分布均勻度,有助于提高傳感器的非理想流場測量性能。因此,需要開展傳感器權(quán)函數(shù)分布規(guī)律的研究。基于有限元軟件COMSOL,分析了4種異徑純水流量計傳感器權(quán)函數(shù)的均勻度,結(jié)果表明:矩形異徑傳感器的權(quán)函數(shù)*均勻。建立矩形異徑純水流量計傳感器三維模型,研究權(quán)函數(shù)與矩形段長寬高的分布規(guī)律,結(jié)果表明:矩形段高度對權(quán)函數(shù)均勻性的影響*大,寬度稍小,長度影響*小。矩形段的高度和寬度越小,權(quán)函數(shù)分布越均勻,測量結(jié)果受非理想流場的影響越小。
引言
異徑純水流量計傳感器由于安裝空間狹小、前后沒有理想直管段,管道內(nèi)被測流場通常是非理想流場,將導(dǎo)致測量值與真實值存在較大偏差、影響計量精度。為提高非理想流場的測量性能,需要研究合適的異徑截面形狀和尺寸,以提高傳感器內(nèi)權(quán)函數(shù)分布的均勻度。然而國內(nèi)外相關(guān)的研究較少。ShercliffJA和BevirMK等人*次提出和深化了純水流量計的權(quán)函數(shù)理論。衛(wèi)開夏等人利用ANSYS有限元軟件求解非滿管純水流量計的權(quán)函數(shù)分布。孔令富等人使用MATLAB軟件中的PDE工具箱對權(quán)函數(shù)進行有限元求解。王月明等人基于ANSYS對含有非導(dǎo)電物質(zhì)時的純水流量計進行有限元分析。李雪菁采用COMSOLMultiphysics有限元軟件求解非絕緣管純水流量計的權(quán)函數(shù)分布。王經(jīng)卓等人基于COMSOL軟件,利用流體像素的方法求解純水流量計權(quán)函數(shù)的分布。上述文獻主要針對圓管純水流量計傳感器點電*的二維權(quán)函數(shù)進行分析,其研究結(jié)果與實際三維情況存在偏差。同時,尚未有人針對異徑純水流量計傳感器三維權(quán)函數(shù)的分布規(guī)律進行研究。由于無可參考的非理想流場測量工況的理論依據(jù),研發(fā)人員無法確定究竟何種異徑截面有助于提高權(quán)函數(shù)均勻度,也無法確定哪一種尺寸有助于提高權(quán)函數(shù)均勻度。針對這一問題,本文從理論上研究權(quán)函數(shù)與耦合電動勢關(guān)系,確定提高權(quán)函數(shù)分布均勻度有助于非理想流場測量。通過COMSOL軟件采用電場模擬法,分析4種不同異徑截面純水流量計傳感器的權(quán)函數(shù)分布均勻度,確定較優(yōu)的異徑截面形狀。針對優(yōu)選異徑截面形狀的圓電*純水流量計傳感器,研究權(quán)函數(shù)分布均勻度與異徑段長寬高之間的規(guī)律。所得結(jié)論為異徑純水流量計傳感器的測量管結(jié)構(gòu)尺寸設(shè)計提供了一定的參考,也為提高異徑純水流量計傳感器的非理想流場測量性能提供了理論依據(jù)。
1、純水流量計傳感器檢測原理
當(dāng)導(dǎo)電性液體在磁場中作切割磁力線運動時,液體中有感應(yīng)電流產(chǎn)生。假定液體的電導(dǎo)率δ是均勻、各向同性的,則歐姆定律的普遍公式寫作

式中j→為電流密度矢量,為通過液體單位面積的電流,A/m2;E→為電場強度矢量,V/m;v→為流體速度,m/s;B→為磁感應(yīng)強度,T。當(dāng)激勵電流角頻率ω不大時,流體中的位移電流完全可以忽略,即
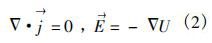
將式(2)帶入式(1)得純水流量計傳感器的基本測量方程
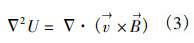
式中U為感應(yīng)電動勢,V;2為拉普拉斯算子;為哈密頓算子。
通常借助Green函數(shù)G來求解微分方程(3),G滿足Laplace方程
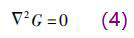
根據(jù)傳感器的管道形狀和電絕緣邊界條件,建立了完整形式的純水流量計傳感器基本方程
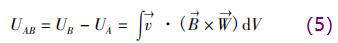
式中V為純水流量計傳感器測量空間;W→為權(quán)函數(shù)。在直角坐標系(x,y,z)中,式(5)可以轉(zhuǎn)換為
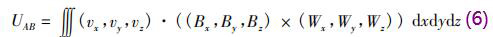
若磁感應(yīng)強度在傳感器有效工作區(qū)間內(nèi)分布均勻,則磁感應(yīng)強度B=By,Bx=Bz=0,式(6)可以化為
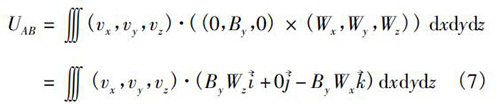
當(dāng)流速為軸向流時,即v=-vz,vx=vy=0;則式(7)表示為
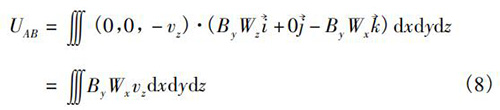
同時,若傳感器內(nèi)的權(quán)函數(shù)分布均勻,Wx=W,則式(8)變?yōu)?br />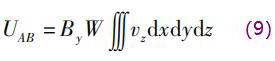
傳感器內(nèi)的權(quán)函數(shù)分布均勻時,感應(yīng)電動勢大小只與流速積分值成正比,不依賴于流型的分布,有利于非理想流場的精確測量。
2權(quán)函數(shù)仿真與分析
純水流量計傳感器內(nèi)的流體微元切割磁力線產(chǎn)生感應(yīng)的電勢和電位,相當(dāng)于一個個微小的“電源”。某一點的權(quán)函數(shù)應(yīng)為該點微元作為“電源”所產(chǎn)生的電位梯度與電*間電位差之比。所以,可以采用電場模擬法測定權(quán)函數(shù):傳感器空間內(nèi)充滿導(dǎo)電液體(一般為水),在電*處施加一定的電壓,便會在導(dǎo)電介質(zhì)中形成一個電場,測得各點的電場強度,并除以中心點的電場強度,即得到歸一化后的權(quán)函數(shù)值,將其繪制成等值線圖便可得到權(quán)函數(shù)分布圖。
2.1仿真方法
基于電場模擬法,選擇COMSOLMultiphysics有限元仿真軟件求解權(quán)函數(shù)步驟如下:
1)使用AC/DC模塊中的電流應(yīng)用程序模式,圓管半徑為32mm,點電*半徑0.4mm,仿真模型為二維模型;
2)電*材質(zhì)設(shè)置為金屬銅,導(dǎo)電液體為水,電導(dǎo)率為1×10-4S/m;
3)測量管具有絕緣襯里,滿足電絕緣邊界條件n→×j→=0,左右電*分別施加1,-1V的電壓;
4)劃分四邊形網(wǎng)格,為了保證仿真結(jié)果的精確度,選擇*細化網(wǎng)格;
5)使用穩(wěn)態(tài)求解器進行計算,得到各點處的電場強度,并除以中心點處的電場強度,得到歸一化后的權(quán)函數(shù)值。
2.2結(jié)果分析
2.2.1不同異徑面的影響
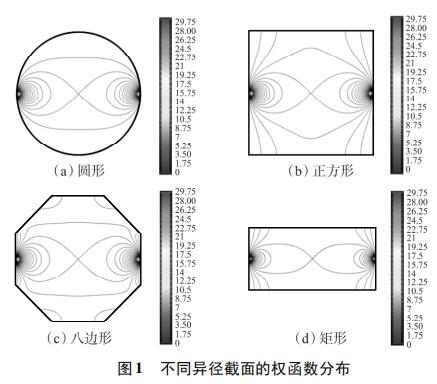
為考察不同異徑截面權(quán)函數(shù)分布的均勻性,使用上述方法對圓形、正方形、八邊形和矩形異徑截面的權(quán)函數(shù)分布進行定性分析。為了便于對比,設(shè)置管道口徑為DN100,異徑部分截面積為3200mm2。所以,圓形異徑面半徑為32mm,正方形異徑面邊長為56.6mm,八邊形異徑面邊長為25.8mm,矩形異徑面長寬為80×40mm。仿真結(jié)果如圖1所示,為了便于對比,權(quán)函數(shù)等勢線大小從0開始,以0.25為步長遞增到30。由圖1(a)~圖1(d)可知,矩形異徑截面的權(quán)函數(shù)等勢線間距*大,即權(quán)函數(shù)變化梯度*小,權(quán)函數(shù)分布*均勻。
為了客觀評價不同異徑截面內(nèi)權(quán)函數(shù)分布的均勻程度,采用整體均勻度來定量衡量權(quán)函數(shù)的均勻性,設(shè)電*截面內(nèi)每個節(jié)點的權(quán)函數(shù)值為 Wk,相應(yīng)截面的權(quán)函數(shù)平均值為 W0,則電*截面內(nèi)權(quán)函數(shù)的整體均勻度 R 為
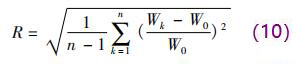
通過式( 10) 計算得到圓形、正方形、八邊形、矩形 4 種
不同異徑截面權(quán)函數(shù)分布的整體均勻度分別為 1. 811 2, 1. 996 9,1. 915 0,1. 563 9。
綜上所述,矩形異徑結(jié)構(gòu)的權(quán)函數(shù)分布*均勻,所以,異徑純水流量計傳感器采用矩形異徑的管道結(jié)構(gòu),該結(jié)構(gòu)權(quán)函數(shù)分布比較均勻,能夠減少非理想流場引入的測量誤差。在實際生產(chǎn)實踐過程中,權(quán)函數(shù)分布與矩形段長 L、寬 D、 高 H 有關(guān),因此,開展了矩形異徑圓電*純水流量計傳感器的三維權(quán)函數(shù)建模分析,*終得到一種權(quán)函數(shù)分布比較均勻的結(jié)構(gòu)尺寸。
2. 2. 2 三維權(quán)函數(shù)分布
使用 Pro /E 軟件建立三維幾何模型,導(dǎo)入 COMSOL 軟件進行有限元求解。仿真模型如圖 2 所示,電*連線為x 軸,連線中點為坐標原點,流體運動方向為 z 軸,傳感器管道口徑為 DN100,總長250 mm。異徑管部分初始結(jié)構(gòu)尺寸 L = 80 mm,D = 80 mm,H = 40 mm,圓形電*半徑為17 mm,伸出絕緣襯里的*大距離為 1. 5 mm。
1) 長度的影響

*先分析一定 D × H 條件下,L 變化時傳感器內(nèi)的權(quán)函數(shù)分布情況。由于傳感器異徑管部分高度 H 越小信號越強,但壓損也越大,因此,H 設(shè)置為 30 ~ 50 mm; 異徑管寬度 D 越大壓損越小,但寬度越大傳感器體積也越大,所以, D 設(shè)置為 60 ~ 90 mm; 異徑管段上下需要放置激勵線圈,同時異徑段前后需要有一定長度的過渡段來穩(wěn)定流型,因此, L 設(shè)置為 60 ~ 120 mm。一共分析了 6 組 D × H 尺寸的傳感器權(quán)函數(shù)分布隨 L 的變化情況,如表 2 所示。由于電*截面內(nèi)的權(quán)函數(shù)分布對感應(yīng)電動勢影響*大,因 此,利 用式( 10) 計算電*截面 xy 平面內(nèi)的權(quán)函數(shù)整體均勻度 R。定義相同 D × H 條件下,權(quán)函數(shù)均勻度隨 L 變化的波動率為 ML,如下
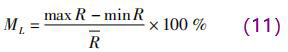
計算多組相同 D × H、不同 L 時 xy 平面的權(quán)函數(shù)整體均勻度 R 及波動率 ML,如表 1 所示。

通過表 1 分析可知,隨著 L 的變化,權(quán)函數(shù)波動率ML≤ ±2. 5 % ,所以 xy 平面內(nèi)的權(quán)函數(shù)整體均勻度變化較小,即長度 L 對電*截面內(nèi)的權(quán)函數(shù)分布影響很小。
2) 寬度和高度的影響
通過上述分析可知,L 對傳感器內(nèi)的權(quán)函數(shù)分布影響很小,因此固定設(shè)置 L 為 80 mm。然后分析異徑段 D,H 同時變化時的權(quán)函數(shù)分布情況。由上節(jié)可知,矩形異徑截面的 D 設(shè)置為 60 ~ 90 mm,H 設(shè)置為 30 ~ 50 mm。為了便于分析三維權(quán)函數(shù)與 D,H 的變化關(guān)系,設(shè)置 H 與 D 變化步長都是 10 mm,因此,H 變化范圍為 30 ~ 60 mm,即 D = { 60,70, 80,90 mm} ,H = { 30,40,50,60 mm} ,一共 16 組異徑純水流量計傳感器結(jié)構(gòu)。
分別對上述結(jié)構(gòu)進行有限元分析,根據(jù)式( 10) 計算 xy平面內(nèi)權(quán)函數(shù)整體均勻度 R,根據(jù)式( 11) 計算權(quán)函數(shù)隨 H變化的波動率 MH,隨 D 變化的波動率 MD,結(jié)果如表 2 所 示。
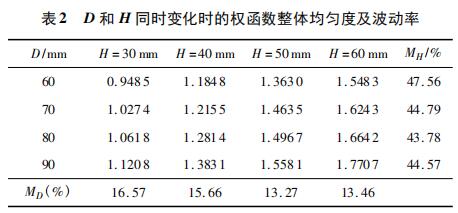
根據(jù)表 1 和表 2 權(quán)函數(shù)均勻度的波動率數(shù)值可以看出,MH > MD > ML,所以,矩形段 L,D,H 對于權(quán)函數(shù)均勻度的影響程度是依次增強的,高度 H 對權(quán)函數(shù)均勻度影響*大,寬度 D 影響稍小,長度 L 影響很小。且 D 和 H 越小,權(quán)函數(shù)整體均勻度 R 越小,權(quán)函數(shù)分布越均勻。
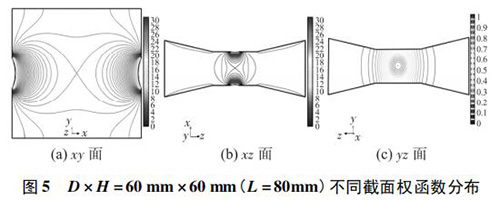
為了更加全面地比較權(quán)函數(shù)在三維空間的分布情況,從上述結(jié)構(gòu)中選取 D × H = { 90 × 30,60 × 30,60 × 60} 三組典型結(jié)構(gòu),分析其權(quán)函數(shù)在 xy,xz,yz 三個平面內(nèi)的分布情況。為了便于對比,統(tǒng)一規(guī)定三個平面內(nèi)等勢線的分布步長和數(shù)值范圍: 1) xy,xz 平面內(nèi)的權(quán)函數(shù)等勢線大小以0. 25為步長,從 0 增加到 30; 2) 由于 yz 平面的權(quán)函數(shù)小于1,規(guī)定 yz 平面內(nèi)的權(quán)函數(shù)等勢線大小以 0. 05 為步長,從 0增加到 1。具體如圖 3 ~ 圖 5 所示

通過對圖 3 ~ 圖 5 分析得出以下結(jié)論: 1) 圖 3( a) 、圖 4( a) 的 xy 面權(quán)函數(shù)分布表明,D = 90 mm時中心區(qū)域的權(quán)函數(shù)等勢線間距較大,即權(quán)函數(shù)變化梯度較小,且中心區(qū)域的權(quán)函數(shù)等勢線逐漸變?yōu)橹本€,因此中心區(qū)域的權(quán)函數(shù)分布更均勻; 但 D = 90 mm 時,電*附近的權(quán)函數(shù)等勢線較密,且等勢線顏色較深,權(quán)函數(shù)*大值較大,變化梯度較大,所以,電*附近的權(quán)函數(shù)分布均勻性較差。因為難以直接衡量 D 改變時,xy 面權(quán)函數(shù)分布的均勻性。所以,需要利用權(quán)函數(shù)整體均勻度 R 定量確定 xy 平面內(nèi)權(quán)函數(shù)分布的均勻性。結(jié)果表明,隨著寬度 D 的減小,權(quán)函數(shù)分布越來越均勻。
2) 圖 4( a) 、圖 5( a) 的 xy 面權(quán)函數(shù)分布表明,H = 30 mm時中心區(qū)域的權(quán)函數(shù)等勢線間距較大,且中心區(qū)域的權(quán)函數(shù)等勢線逐漸變?yōu)橹本€; 電*附近的權(quán)函數(shù)等勢線比較稀疏,且等勢線顏色較淺,權(quán)函數(shù)*大值較小,變化梯度小,因 此,H = 30 mm 時 xy 面的權(quán)函數(shù)分布更加均勻。
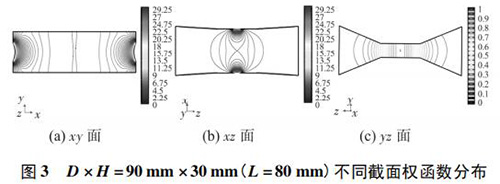
3) 圖 3( b) ~ 5( b) 的 xz 面權(quán)函數(shù)分布表明,三組異徑結(jié)構(gòu)的權(quán)函數(shù)分布情況類似,沒有明顯的區(qū)別,即 D 和 H的變化對 xz 面的權(quán)函數(shù)分布影響較小。
4) 圖 3( c) 、圖 4( c) 的 yz 面權(quán)函數(shù)分布表明,D = 90 mm時的權(quán)函數(shù)等勢線間距略大于 D = 60 mm 時的權(quán)函數(shù)等勢線間距,權(quán)函數(shù)變化梯度較小,且中心區(qū)域的權(quán)函數(shù)等勢線逐漸變?yōu)橹本€,因此 D = 90 mm 的權(quán)函數(shù)分布更均勻一些,但是兩者區(qū)別很小,即寬度改變對 yz 面權(quán)函數(shù)分布影響很小。圖 4( c) 、圖 5( c) 的 yz 面權(quán)函數(shù)分布表明,H = 30 mm時的權(quán)函數(shù)等勢線間距較大,且中心區(qū)域的權(quán)函數(shù)等勢線逐漸變?yōu)橹本€,因此 H = 30 mm 的權(quán)函數(shù)分布更加均勻;
5) 圖 3( a) ~ 5( a) 和圖 3( b) ~ 5( b) 權(quán)函數(shù)分布結(jié)果表明,越靠近電*,等勢線顏色越深,即權(quán)函數(shù)值越大,且越靠近電*,權(quán)函數(shù)等勢線越密集,即權(quán)函數(shù)變化梯度越大。
綜上所述,異徑電磁水表異徑段長度 L 對權(quán)函數(shù)分布的均勻性影響很小,隨著長度 L 的改變,權(quán)函數(shù)分布基本沒有變化; 異徑段高度 H 對權(quán)函數(shù)分布的均勻性影響*大,寬度 D 影響稍小,高度和寬度越小,權(quán)函數(shù)分布越均勻,即異徑純水流量計傳感器的測量精確度受非理想流場的影響越小。
3 結(jié) 論
1) 圓形、正方形、八邊形和矩形等 4 種異徑純水流量計傳感器的權(quán)函數(shù)分析結(jié)果表明,矩形異徑截面?zhèn)鞲衅鞯臋?quán)函數(shù)分布*均勻。
2) 電*附近區(qū)域,權(quán)函數(shù)值較大,且權(quán)函數(shù)變化梯度較大,隨著遠離電*,權(quán)函數(shù)值越來越小,且權(quán)函數(shù)變化梯度越來越小。
3) 矩形段高度 H 對權(quán)函數(shù)分布的均勻性影響*大,隨 著 H 的減小,權(quán)函數(shù)分布越來越均勻,且 y 軸權(quán)函數(shù)的分布逐漸趨近于常數(shù) 1。矩形段寬度 D 對權(quán)函數(shù)分布的均勻性影響稍小,隨著 D 的減小,權(quán)函數(shù)分布越來越均勻。矩形段長度 L 對傳感器內(nèi)的權(quán)函數(shù)分布影響很小,隨著 L 的改變,權(quán)函數(shù)分布沒有明顯變化。
衛(wèi)生級純水流量計在測量管道流體脈動流時的特性規(guī)律
純水流量計投入使用時的注意事項及常見故障排除
影響純水流量計使用測量精度的因素有哪些
測量純水流量計在現(xiàn)場使用中常見的問題及解決辦法
純水流量計在選用安裝過程中的注意事項及故障處理
純水流量計傳感器檢測原理及權(quán)函數(shù)仿真與分析
超純水流量計的概述與在人機界面的應(yīng)用
測量純水用什么流量計
帶遠傳純水流量計,純水水流量計
工業(yè)純水流量計,純水流量計價格
衛(wèi)生級純水流量計,機械純水流量計
超純水流量計,測量純水流量計
測量純水用什么流量計,超純水流量計
純水流量計的組成結(jié)構(gòu)與工作原理
純水流量計如何正確選型
純水流量計表頭上面的數(shù)字怎么看
純水流量表如何正確接線圖解
引言
異徑純水流量計傳感器由于安裝空間狹小、前后沒有理想直管段,管道內(nèi)被測流場通常是非理想流場,將導(dǎo)致測量值與真實值存在較大偏差、影響計量精度。為提高非理想流場的測量性能,需要研究合適的異徑截面形狀和尺寸,以提高傳感器內(nèi)權(quán)函數(shù)分布的均勻度。然而國內(nèi)外相關(guān)的研究較少。ShercliffJA和BevirMK等人*次提出和深化了純水流量計的權(quán)函數(shù)理論。衛(wèi)開夏等人利用ANSYS有限元軟件求解非滿管純水流量計的權(quán)函數(shù)分布。孔令富等人使用MATLAB軟件中的PDE工具箱對權(quán)函數(shù)進行有限元求解。王月明等人基于ANSYS對含有非導(dǎo)電物質(zhì)時的純水流量計進行有限元分析。李雪菁采用COMSOLMultiphysics有限元軟件求解非絕緣管純水流量計的權(quán)函數(shù)分布。王經(jīng)卓等人基于COMSOL軟件,利用流體像素的方法求解純水流量計權(quán)函數(shù)的分布。上述文獻主要針對圓管純水流量計傳感器點電*的二維權(quán)函數(shù)進行分析,其研究結(jié)果與實際三維情況存在偏差。同時,尚未有人針對異徑純水流量計傳感器三維權(quán)函數(shù)的分布規(guī)律進行研究。由于無可參考的非理想流場測量工況的理論依據(jù),研發(fā)人員無法確定究竟何種異徑截面有助于提高權(quán)函數(shù)均勻度,也無法確定哪一種尺寸有助于提高權(quán)函數(shù)均勻度。針對這一問題,本文從理論上研究權(quán)函數(shù)與耦合電動勢關(guān)系,確定提高權(quán)函數(shù)分布均勻度有助于非理想流場測量。通過COMSOL軟件采用電場模擬法,分析4種不同異徑截面純水流量計傳感器的權(quán)函數(shù)分布均勻度,確定較優(yōu)的異徑截面形狀。針對優(yōu)選異徑截面形狀的圓電*純水流量計傳感器,研究權(quán)函數(shù)分布均勻度與異徑段長寬高之間的規(guī)律。所得結(jié)論為異徑純水流量計傳感器的測量管結(jié)構(gòu)尺寸設(shè)計提供了一定的參考,也為提高異徑純水流量計傳感器的非理想流場測量性能提供了理論依據(jù)。
1、純水流量計傳感器檢測原理
當(dāng)導(dǎo)電性液體在磁場中作切割磁力線運動時,液體中有感應(yīng)電流產(chǎn)生。假定液體的電導(dǎo)率δ是均勻、各向同性的,則歐姆定律的普遍公式寫作

式中j→為電流密度矢量,為通過液體單位面積的電流,A/m2;E→為電場強度矢量,V/m;v→為流體速度,m/s;B→為磁感應(yīng)強度,T。當(dāng)激勵電流角頻率ω不大時,流體中的位移電流完全可以忽略,即
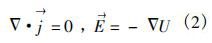
將式(2)帶入式(1)得純水流量計傳感器的基本測量方程
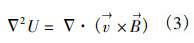
式中U為感應(yīng)電動勢,V;2為拉普拉斯算子;為哈密頓算子。
通常借助Green函數(shù)G來求解微分方程(3),G滿足Laplace方程
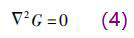
根據(jù)傳感器的管道形狀和電絕緣邊界條件,建立了完整形式的純水流量計傳感器基本方程
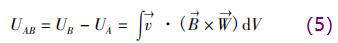
式中V為純水流量計傳感器測量空間;W→為權(quán)函數(shù)。在直角坐標系(x,y,z)中,式(5)可以轉(zhuǎn)換為
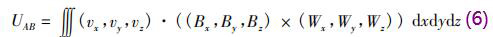
若磁感應(yīng)強度在傳感器有效工作區(qū)間內(nèi)分布均勻,則磁感應(yīng)強度B=By,Bx=Bz=0,式(6)可以化為
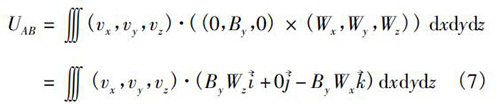
當(dāng)流速為軸向流時,即v=-vz,vx=vy=0;則式(7)表示為
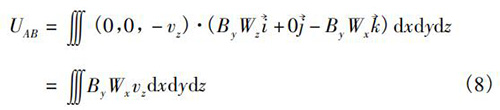
同時,若傳感器內(nèi)的權(quán)函數(shù)分布均勻,Wx=W,則式(8)變?yōu)?br />
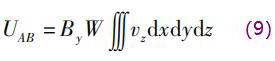
傳感器內(nèi)的權(quán)函數(shù)分布均勻時,感應(yīng)電動勢大小只與流速積分值成正比,不依賴于流型的分布,有利于非理想流場的精確測量。
2權(quán)函數(shù)仿真與分析
純水流量計傳感器內(nèi)的流體微元切割磁力線產(chǎn)生感應(yīng)的電勢和電位,相當(dāng)于一個個微小的“電源”。某一點的權(quán)函數(shù)應(yīng)為該點微元作為“電源”所產(chǎn)生的電位梯度與電*間電位差之比。所以,可以采用電場模擬法測定權(quán)函數(shù):傳感器空間內(nèi)充滿導(dǎo)電液體(一般為水),在電*處施加一定的電壓,便會在導(dǎo)電介質(zhì)中形成一個電場,測得各點的電場強度,并除以中心點的電場強度,即得到歸一化后的權(quán)函數(shù)值,將其繪制成等值線圖便可得到權(quán)函數(shù)分布圖。
2.1仿真方法
基于電場模擬法,選擇COMSOLMultiphysics有限元仿真軟件求解權(quán)函數(shù)步驟如下:
1)使用AC/DC模塊中的電流應(yīng)用程序模式,圓管半徑為32mm,點電*半徑0.4mm,仿真模型為二維模型;
2)電*材質(zhì)設(shè)置為金屬銅,導(dǎo)電液體為水,電導(dǎo)率為1×10-4S/m;
3)測量管具有絕緣襯里,滿足電絕緣邊界條件n→×j→=0,左右電*分別施加1,-1V的電壓;
4)劃分四邊形網(wǎng)格,為了保證仿真結(jié)果的精確度,選擇*細化網(wǎng)格;
5)使用穩(wěn)態(tài)求解器進行計算,得到各點處的電場強度,并除以中心點處的電場強度,得到歸一化后的權(quán)函數(shù)值。
2.2結(jié)果分析
2.2.1不同異徑面的影響
為考察不同異徑截面權(quán)函數(shù)分布的均勻性,使用上述方法對圓形、正方形、八邊形和矩形異徑截面的權(quán)函數(shù)分布進行定性分析。為了便于對比,設(shè)置管道口徑為DN100,異徑部分截面積為3200mm2。所以,圓形異徑面半徑為32mm,正方形異徑面邊長為56.6mm,八邊形異徑面邊長為25.8mm,矩形異徑面長寬為80×40mm。仿真結(jié)果如圖1所示,為了便于對比,權(quán)函數(shù)等勢線大小從0開始,以0.25為步長遞增到30。由圖1(a)~圖1(d)可知,矩形異徑截面的權(quán)函數(shù)等勢線間距*大,即權(quán)函數(shù)變化梯度*小,權(quán)函數(shù)分布*均勻。

為了客觀評價不同異徑截面內(nèi)權(quán)函數(shù)分布的均勻程度,采用整體均勻度來定量衡量權(quán)函數(shù)的均勻性,設(shè)電*截面內(nèi)每個節(jié)點的權(quán)函數(shù)值為 Wk,相應(yīng)截面的權(quán)函數(shù)平均值為 W0,則電*截面內(nèi)權(quán)函數(shù)的整體均勻度 R 為
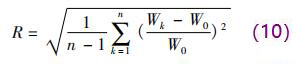
通過式( 10) 計算得到圓形、正方形、八邊形、矩形 4 種
不同異徑截面權(quán)函數(shù)分布的整體均勻度分別為 1. 811 2, 1. 996 9,1. 915 0,1. 563 9。
綜上所述,矩形異徑結(jié)構(gòu)的權(quán)函數(shù)分布*均勻,所以,異徑純水流量計傳感器采用矩形異徑的管道結(jié)構(gòu),該結(jié)構(gòu)權(quán)函數(shù)分布比較均勻,能夠減少非理想流場引入的測量誤差。在實際生產(chǎn)實踐過程中,權(quán)函數(shù)分布與矩形段長 L、寬 D、 高 H 有關(guān),因此,開展了矩形異徑圓電*純水流量計傳感器的三維權(quán)函數(shù)建模分析,*終得到一種權(quán)函數(shù)分布比較均勻的結(jié)構(gòu)尺寸。
2. 2. 2 三維權(quán)函數(shù)分布
使用 Pro /E 軟件建立三維幾何模型,導(dǎo)入 COMSOL 軟件進行有限元求解。仿真模型如圖 2 所示,電*連線為x 軸,連線中點為坐標原點,流體運動方向為 z 軸,傳感器管道口徑為 DN100,總長250 mm。異徑管部分初始結(jié)構(gòu)尺寸 L = 80 mm,D = 80 mm,H = 40 mm,圓形電*半徑為17 mm,伸出絕緣襯里的*大距離為 1. 5 mm。
1) 長度的影響

*先分析一定 D × H 條件下,L 變化時傳感器內(nèi)的權(quán)函數(shù)分布情況。由于傳感器異徑管部分高度 H 越小信號越強,但壓損也越大,因此,H 設(shè)置為 30 ~ 50 mm; 異徑管寬度 D 越大壓損越小,但寬度越大傳感器體積也越大,所以, D 設(shè)置為 60 ~ 90 mm; 異徑管段上下需要放置激勵線圈,同時異徑段前后需要有一定長度的過渡段來穩(wěn)定流型,因此, L 設(shè)置為 60 ~ 120 mm。一共分析了 6 組 D × H 尺寸的傳感器權(quán)函數(shù)分布隨 L 的變化情況,如表 2 所示。由于電*截面內(nèi)的權(quán)函數(shù)分布對感應(yīng)電動勢影響*大,因 此,利 用式( 10) 計算電*截面 xy 平面內(nèi)的權(quán)函數(shù)整體均勻度 R。定義相同 D × H 條件下,權(quán)函數(shù)均勻度隨 L 變化的波動率為 ML,如下
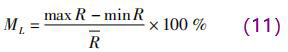
計算多組相同 D × H、不同 L 時 xy 平面的權(quán)函數(shù)整體均勻度 R 及波動率 ML,如表 1 所示。

通過表 1 分析可知,隨著 L 的變化,權(quán)函數(shù)波動率ML≤ ±2. 5 % ,所以 xy 平面內(nèi)的權(quán)函數(shù)整體均勻度變化較小,即長度 L 對電*截面內(nèi)的權(quán)函數(shù)分布影響很小。
2) 寬度和高度的影響
通過上述分析可知,L 對傳感器內(nèi)的權(quán)函數(shù)分布影響很小,因此固定設(shè)置 L 為 80 mm。然后分析異徑段 D,H 同時變化時的權(quán)函數(shù)分布情況。由上節(jié)可知,矩形異徑截面的 D 設(shè)置為 60 ~ 90 mm,H 設(shè)置為 30 ~ 50 mm。為了便于分析三維權(quán)函數(shù)與 D,H 的變化關(guān)系,設(shè)置 H 與 D 變化步長都是 10 mm,因此,H 變化范圍為 30 ~ 60 mm,即 D = { 60,70, 80,90 mm} ,H = { 30,40,50,60 mm} ,一共 16 組異徑純水流量計傳感器結(jié)構(gòu)。
分別對上述結(jié)構(gòu)進行有限元分析,根據(jù)式( 10) 計算 xy平面內(nèi)權(quán)函數(shù)整體均勻度 R,根據(jù)式( 11) 計算權(quán)函數(shù)隨 H變化的波動率 MH,隨 D 變化的波動率 MD,結(jié)果如表 2 所 示。

根據(jù)表 1 和表 2 權(quán)函數(shù)均勻度的波動率數(shù)值可以看出,MH > MD > ML,所以,矩形段 L,D,H 對于權(quán)函數(shù)均勻度的影響程度是依次增強的,高度 H 對權(quán)函數(shù)均勻度影響*大,寬度 D 影響稍小,長度 L 影響很小。且 D 和 H 越小,權(quán)函數(shù)整體均勻度 R 越小,權(quán)函數(shù)分布越均勻。
為了更加全面地比較權(quán)函數(shù)在三維空間的分布情況,從上述結(jié)構(gòu)中選取 D × H = { 90 × 30,60 × 30,60 × 60} 三組典型結(jié)構(gòu),分析其權(quán)函數(shù)在 xy,xz,yz 三個平面內(nèi)的分布情況。為了便于對比,統(tǒng)一規(guī)定三個平面內(nèi)等勢線的分布步長和數(shù)值范圍: 1) xy,xz 平面內(nèi)的權(quán)函數(shù)等勢線大小以0. 25為步長,從 0 增加到 30; 2) 由于 yz 平面的權(quán)函數(shù)小于1,規(guī)定 yz 平面內(nèi)的權(quán)函數(shù)等勢線大小以 0. 05 為步長,從 0增加到 1。具體如圖 3 ~ 圖 5 所示

通過對圖 3 ~ 圖 5 分析得出以下結(jié)論: 1) 圖 3( a) 、圖 4( a) 的 xy 面權(quán)函數(shù)分布表明,D = 90 mm時中心區(qū)域的權(quán)函數(shù)等勢線間距較大,即權(quán)函數(shù)變化梯度較小,且中心區(qū)域的權(quán)函數(shù)等勢線逐漸變?yōu)橹本€,因此中心區(qū)域的權(quán)函數(shù)分布更均勻; 但 D = 90 mm 時,電*附近的權(quán)函數(shù)等勢線較密,且等勢線顏色較深,權(quán)函數(shù)*大值較大,變化梯度較大,所以,電*附近的權(quán)函數(shù)分布均勻性較差。因為難以直接衡量 D 改變時,xy 面權(quán)函數(shù)分布的均勻性。所以,需要利用權(quán)函數(shù)整體均勻度 R 定量確定 xy 平面內(nèi)權(quán)函數(shù)分布的均勻性。結(jié)果表明,隨著寬度 D 的減小,權(quán)函數(shù)分布越來越均勻。
2) 圖 4( a) 、圖 5( a) 的 xy 面權(quán)函數(shù)分布表明,H = 30 mm時中心區(qū)域的權(quán)函數(shù)等勢線間距較大,且中心區(qū)域的權(quán)函數(shù)等勢線逐漸變?yōu)橹本€; 電*附近的權(quán)函數(shù)等勢線比較稀疏,且等勢線顏色較淺,權(quán)函數(shù)*大值較小,變化梯度小,因 此,H = 30 mm 時 xy 面的權(quán)函數(shù)分布更加均勻。

3) 圖 3( b) ~ 5( b) 的 xz 面權(quán)函數(shù)分布表明,三組異徑結(jié)構(gòu)的權(quán)函數(shù)分布情況類似,沒有明顯的區(qū)別,即 D 和 H的變化對 xz 面的權(quán)函數(shù)分布影響較小。
4) 圖 3( c) 、圖 4( c) 的 yz 面權(quán)函數(shù)分布表明,D = 90 mm時的權(quán)函數(shù)等勢線間距略大于 D = 60 mm 時的權(quán)函數(shù)等勢線間距,權(quán)函數(shù)變化梯度較小,且中心區(qū)域的權(quán)函數(shù)等勢線逐漸變?yōu)橹本€,因此 D = 90 mm 的權(quán)函數(shù)分布更均勻一些,但是兩者區(qū)別很小,即寬度改變對 yz 面權(quán)函數(shù)分布影響很小。圖 4( c) 、圖 5( c) 的 yz 面權(quán)函數(shù)分布表明,H = 30 mm時的權(quán)函數(shù)等勢線間距較大,且中心區(qū)域的權(quán)函數(shù)等勢線逐漸變?yōu)橹本€,因此 H = 30 mm 的權(quán)函數(shù)分布更加均勻;
5) 圖 3( a) ~ 5( a) 和圖 3( b) ~ 5( b) 權(quán)函數(shù)分布結(jié)果表明,越靠近電*,等勢線顏色越深,即權(quán)函數(shù)值越大,且越靠近電*,權(quán)函數(shù)等勢線越密集,即權(quán)函數(shù)變化梯度越大。

綜上所述,異徑電磁水表異徑段長度 L 對權(quán)函數(shù)分布的均勻性影響很小,隨著長度 L 的改變,權(quán)函數(shù)分布基本沒有變化; 異徑段高度 H 對權(quán)函數(shù)分布的均勻性影響*大,寬度 D 影響稍小,高度和寬度越小,權(quán)函數(shù)分布越均勻,即異徑純水流量計傳感器的測量精確度受非理想流場的影響越小。
3 結(jié) 論
1) 圓形、正方形、八邊形和矩形等 4 種異徑純水流量計傳感器的權(quán)函數(shù)分析結(jié)果表明,矩形異徑截面?zhèn)鞲衅鞯臋?quán)函數(shù)分布*均勻。
2) 電*附近區(qū)域,權(quán)函數(shù)值較大,且權(quán)函數(shù)變化梯度較大,隨著遠離電*,權(quán)函數(shù)值越來越小,且權(quán)函數(shù)變化梯度越來越小。
3) 矩形段高度 H 對權(quán)函數(shù)分布的均勻性影響*大,隨 著 H 的減小,權(quán)函數(shù)分布越來越均勻,且 y 軸權(quán)函數(shù)的分布逐漸趨近于常數(shù) 1。矩形段寬度 D 對權(quán)函數(shù)分布的均勻性影響稍小,隨著 D 的減小,權(quán)函數(shù)分布越來越均勻。矩形段長度 L 對傳感器內(nèi)的權(quán)函數(shù)分布影響很小,隨著 L 的改變,權(quán)函數(shù)分布沒有明顯變化。
上一篇:關(guān)于硫酸流量計在采油井中的應(yīng)用研究
下一篇:白酒流量計在定量加水系統(tǒng)設(shè)計及改造方案



